Wstęp
Może się zdarzyć, że chcemy żeby postać sama celowała w przeciwnika lub kierowała się w jego stronę. Najważniejsze jest tu sprawdzanie położenia przeciwnika względem postaci na osiach X i Y.
Pokazuje tu kilka metod określania tego położenia przy użyciu paru prostych funkcji.
Namierzanie to bardzo potężne narzędzie, przydatne przy tworzeniu: sztucznej inteligencji, samonaprowadzających się pocisków i samodzielnego nakierowywania postaci.
Funkcje
Jak już wspomniałem trzeba znać położenie przeciwnika na osiach. Przydatne są do tego funkcje: P2Dist X, P2Dist Y, P2BodyDist X, P2BodyDist Y. Funkcje zwracają dystans, subiektywne położenie względem obiektu który sprawdza to położenie, jednak to w zupełności wystarczy.
Jak sama nazwa wskazuje funkcje P2BodyDist określają położenie tak jak zwykłe P2Dist ale uwzględniając przy okazji rozmiary przeciwnika podane w pliku CNS, między innymi takie jak: ground.front, air.back, itd.
Natomiast zwykłe P2Dist biorą pod uwagę jedynie punkt O osi wewnętrznych przeciwnika.
Do tego wszystkiego należy dodać też funkcje matematyczne: Tan(x) i Atan(x). Co najważniejsze, trzeba pamiętać o odwrotnych wartościach na osi Y, stąd pojawia się nieoczekiwanie minus, kiedy wydaje się, że powinien być plus.
P2Dist X, P2Dist Y - Funkcja zwraca odległość P2 czyli najbliższego przeciwnika na podanej osi od P1 czyli postaci. Dla osi X wartości dodatnie oznaczają że P2 jest przed P1 z przodu, wartości ujemne oznaczają że P2 jest za plecami P1. Dla osi Y wartości ujemne oznaczają że P2 jest nad P1. Funkcja zwraca odległość bez uwzględnienia szerokości postaci, tylko względem głównej osi (Axis).
P2BodyDist X, P2BodyDist Y - Funkcja zwraca odległość z uwzględnieniem szerokości obiektu (body – ciało).
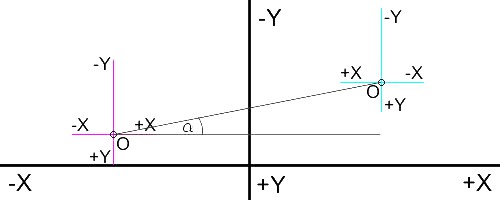
Metoda prostego założenia
Metodę nazwałem w ten sposób, ponieważ można jej użyć w mało skomplikowanych wypadkach. Polega ona na banalnym sprawdzeniu założeń. Przydatne jest to w sytuacjach gdy np. animacja ataku lub sam atak nie jest zbyt rozbudowany i ważne jest czy przeciwnik jest nad, pod lub na równi z postacią. W tej sytuacji wystarczy sprawdzić P2Dist Y.
P2Dist Y < 0 ; Punkt O osi wewnętrznych przeciwnika jest wyżej niż postaci. P2Dist Y = 0 ; Przeciwnik jest na równi z postacią. P2Dist Y > 0 ; Przeciwnik jest niżej.
W ten sposób łatwo sprawdzić czy przeciwnik jest wyżej lub niżej. Każda postać ma swoją wysokość i dla większego realizmu można zwiększyć zakres P2Dist Y o jakieś np. 40 pikseli. Wywoła to taki efekt jakby przesunąć środek osi wewnętrznych przeciwnika nieco wyżej. To nie jest wiele, a jeżeli przeciwnik będzie wyżej lub niżej o te 40 pikseli to zostanie potraktowany jakby był na równi z postacią.
P2Dist Y < -40 ; Przeciwnik jest wyżej niż 40 pikseli od postaci. P2Dist Y = [-40, 40] ; Przeciwnik jest na równi z postacią, od -40 do +40 pikseli włącznie. P2Dist Y > 40 ; Przeciwnik jest niżej niż 40 pikseli.
Przykład:
[State 1, w gore] trigger1 = p2dist Y < -40 type = varset v = 1 value = 2 [State 1, na rowni] trigger1 = p2dist Y = [-40, 40] type = varset v = 1 value = 1 [State 1, w dol] trigger1 = p2dist Y > 40 type = varset v = 1 value = 3
Metoda stosunków odległości
Z poprzedniej metody już wiemy jak określić czy przeciwnik jest np. wyżej. Dobrze, ale teraz jeżeli chcemy wywołać np. atak pod kątem 45o, to nawet kiedy przeciwnik będzie bardzo blisko i jednocześnie bardzo wysoko, to postać nie trafi. W takiej sytuacji trzeba wziąć pod uwagę nie tylko oś Y ale też X. W sytuacji kiedy przykładowo dystans to 100 pikseli na obu osiach mamy do czynienia z kątem 45o, czyli ze stosunkiem jeden do jednego. Wystarczy podzielić przez siebie P2Dist, uznałem że najlepiej będzie wstawić oś Y w mianowniku bo kiedy postać będzie na równi z przeciwnikiem P2Dist Y = 0. Oczywiście P2Dist X też może być równy 0 ale to w 2 sytuacjach, kiedy przeciwnik jest nad lub pod postacią, oczywiście Mugen zasygnalizuje błąd dzielenia przez 0 ale nie wyłączy się. Można dla pewności stosować dodatkowe funkcje albo założenia nie doprowadzające do wykonania dzielenia przez 0.
P2Dist Y / P2Dist X = 1 ; Kiedy dystanse są równe np. 100/100 = 1/1 = jeden do jednego = 1.
Oczywiście ciężko jest natrafić na taki stosunek, więc jak w poprzedniej metodzie musimy stworzyć zakres odpowiednich wartości. Sprawdzać można gotowy stosunek wielkości np. (1/2), (3/1), lub wartość liczbową wynikającą z tego stosunku np. 0.5, 3, itd.
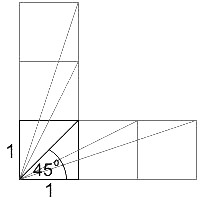
Jak widać metoda ta nie jest zbyt dokładna i posługiwać można się nią na wyczucie. Patrząc na rysunek łatwo stwierdzić, że dążąc do kąta 0o stosunek odległości dąży do 0, podobnie dążąc do kąta 90o stosunek dąży do nieskończoności. Bez zagłębiania się zbędnie w zawiłości obliczania kątów w takiej sytuacji, można patrzeć na rysunek i rozważyć wartości stosunków też w inny sposób. Można przyjąć, że przy kącie 45o mamy do czynienia ze stosunkiem równym 1. Co za tym idzie od kąta 0o do 45o mamy liczby od 0 do 1, czyli dla liczby o połowę mniejszej równej 0.5 mamy kąt 22.5o. Od kąta 45o do 90o mamy liczby od 1 do nieskończoności, więc tak samo dla liczby dwukrotnie większej równej 2 mamy kąt 67.5o. Jak już wspomniałem wszystko to nie oznacza oczywiście że dla liczby 4 kąt będzie wynosił 112.5o a wręcz przeciwnie nadal nie osiągnie 90o, wystarczy zerknąć na rysunek. Kąt będzie wzrastał o miarę wprost proporcjonalnie mniejszą do wzrostu stosunków odległości i podobnie w drugą stronę. Czyli przy stosunku odległości równym 2, kąt wzrośnie o 22.5o czyli będzie 67.5o, ale przy stosunku równym 3 wzrośnie dodatkowo o 11.25o co da 78.75o. Oczywiście kąty te podane są w ogromnym przybliżeniu bo nie można od tak przełożyć kąta na liczbę.
Przykład:
[State 1, w gore 90] trigger1 = p2dist Y / p2dist X < -2 type = varset v = 1 value = 4 [State 1, w gore 45] trigger1 = p2dist Y / p2dist X = [-2, -0.5) type = varset v = 1 value = 2 [State 1, na rowni] trigger1 = p2dist Y / p2dist X = [-0.5, 0.5] type = varset v = 1 value = 1 [State 1, w dol 45] trigger1 = p2dist Y / p2dist X = (0.5, 2] type = varset v = 1 value = 3 [State 1, w dol 90] trigger1 = p2dist Y / p2dist X > 2 type = varset v = 1 value = 5
Metoda kątowa
W poprzedniej metodzie pokazałem jak można z przybliżeniem określić kąt pod jakim jest przeciwnik z punktu widzenia postaci. Jak widać nie jest to tak czytelne jak byśmy chcieli, najłatwiej byłoby po prostu sprawdzać zakres kątowy w którym jest przeciwnik. Miarą jaką będziemy się posługiwali nie będą zwykłe stopnie ale liczba "PI", jak wiadomo pi = 180o. Otwieramy tablice matematyczne i przypominamy sobie, że podczas miary kątów używamy takich funkcji jak: Sin(x), Cos(x) i Tg(x), w Mugenie: Sin(x), Cos(x) i Tan(x).
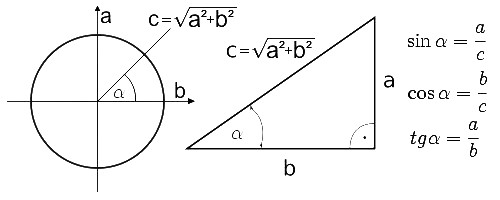
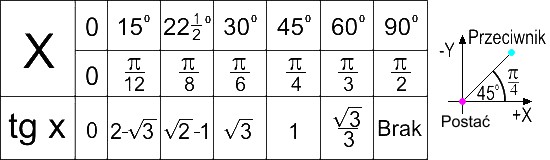
Przy innych funkcjach trzeba znać "przeciwprostokatną" tak jak na rysunku, dla tego najlepiej użyć funkcji Tan(x). Patrząc na koło trygonometryczne i wzory widać podobieństwo do poprzedniej metody, należy też pamiętać, że nie istnieje Tan(90o), więc odpowiednio trzeba go wyłączyć z przedziałów.
tan(x) = P2Dist Y / P2Dist X tan(45o) = tan(pi/4) = 1 ; Tak jak w przypadku poprzedniej metody, kiedy dystanse są równe np. 100/100 = 1/1 = jeden do jednego = 1.
Metoda kątowa trygonometryczna
Tak jak wszędzie musimy najpierw wywołać działanie a potem sprawdzić czy zgadza się z wynikiem np. x + 1 = 2, tu jest identycznie, nie można najpierw podać kąta i wykonać dzielenia P2Dist, tylko podzielić i sprawdzić czy wynik jest zgodny z wartością zwracaną przez funkcję Tan(x).
P2Dist Y / P2Dist X = tan(0) ; Przeciwnik na równi z postacią. P2Dist Y / P2Dist X = tan(pi/4) ; Przeciwnik pod kątem 45o w dół.
Oczywiście jak w metodach poprzednich ciężko jest tak sprawdzać wszystkie kąty, więc zbudujemy przedziały.
P2Dist Y / P2Dist X = [-tan(pi/12),tan(pi/12)] ; Sprawdzamy czy przeciwnik jest pod kątem od -15o (u góry) do +15o (u dołu).
Przykład:
[State 1, w gore do 90] trigger1 = p2dist Y / p2dist X = (-tan(pi/2),-tan(pi/3)] trigger2 = p2dist X = 0 && p2dist Y < 0 type = varset v = 1 value = 4 [State 1, w gore 45] trigger1 = p2dist Y / p2dist X = (-tan(pi/3),-tan(pi/8)] type = varset v = 1 value = 2 [State 1, na rowni] trigger1 = p2dist Y / p2dist X = (-tan(pi/8),tan(pi/8)) type = varset v = 1 value = 1 [State 1, w dol 45] trigger1 = p2dist Y / p2dist X = [tan(pi/8),tan(pi/3)] type = varset v = 1 value = 3 [State 1, w dol do 90] trigger1 = p2dist Y / p2dist X = [tan(pi/3),tan(pi/2)) trigger2 = p2dist X = 0 && p2dist Y > 0 type = varset v = 1 value = 5
Metoda kątowa cyklometryczna
Funkcje cyklometryczne to funkcje odwrotne do funkcji trygonometrycznych, nie ma w tym wielkiej filozofii, odpowiednikiem tg(x) jest arctg(x) (arcus tangens), w Mugenie: Atan(x).
tg(x) = P2Dist Y / P2Dist X tg(pi/4) = 1 arctg(P2Dist Y / P2Dist X) = x arctg(1) = pi/4
W poprzedniej sytuacji nie można było użyć takiego zapisu, bo tg(pi/4) = 1, ale tg(1) to nie jest pi/4. Wszystko działa na tych samych zasadach z tym, że działania są bardziej przejrzyste. Dodatkowo ponieważ oś Y jest odwrócona, proponuje wstawianie minusa przed P2Dist Y kiedy sprawdzać będziemy położenie nad postacią, to jeszcze bardziej ułatwi przeglądanie kodu.
Atan(P2Dist Y / P2Dist X) = 0 ; Przeciwnik na równi z postacią. Atan(P2Dist Y / P2Dist X) = pi/4 ; Przeciwnik pod kątem 45o w dół. Atan(P2Dist Y / P2Dist X) = [-pi/12, pi/12] ; Sprawdzamy czy przeciwnik jest pod kątem od -15o (u góry) do +15o (u dołu).
Przykład:
[State 1, w gore do 90] trigger1 = Atan(-p2dist Y / p2dist X) = [pi/3,pi/2) trigger2 = p2dist X = 0 && p2dist Y < 0 type = varset v = 1 value = 4 [State 1, w gore 45] trigger1 = Atan(-p2dist Y / p2dist X) = [pi/8,pi/3) type = varset v = 1 value = 2 [State 1, na rowni] trigger1 = Atan(p2dist Y / p2dist X) = (-pi/8,pi/8) type = varset v = 1 value = 1 [State 1, w dol 45] trigger1 = Atan(p2dist Y / p2dist X) = [pi/8,pi/3) type = varset v = 1 value = 3 [State 1, w dol do 90] trigger1 = Atan(p2dist Y / p2dist X) = [pi/3,pi/2) trigger2 = p2dist X = 0 && p2dist Y > 0 type = varset v = 1 value = 5

 Infinity MUGEN
Infinity MUGEN
